Capítulo 1 Espaços de Probabilidade

Neste capítulo formulamos um modelo matemático (ou modelo probabilístico) para um experimento aleatório. Começamos definindo o que é um experimento aleatório.

Definição 1.1 Um experimento é aleatório se, quando repetido sob as mesmas condições nem sempre gera os mesmos resultados, isto é, não conseguimos prever o resultado do experimento até que ele seja realizado.

Exemplos de experimentos aleatorios

1. Lançar um dado e registrar a face superior.

2. Contar o número de pessoas que chegam numa agência bancária durante um período de tempo dado.

3. Medir o tempo de vida útil, em horas, de uma lâmpada.

A seguir descreveremos o modelo probabilistíco para um experimento aleatório.

1.1 Espaço amostral

Definição 1.2 (Espaço amostral) O conjunto de todos os resultados possíveis de um experimento aleatório é chamado de espaço amostral, e o denotamos por \(\Omega\).

A continuação apresentamos um espaço amostral adequado para cada um dos experientos descritos nos exemplos acima:

1. \(\Omega = \{1,2,3,4,5,6\}\).

2. \(\Omega = \{0,1,2,3,\ldots\}\)

3. \(\Omega = \{x \in \mathbb R : 0\leq x < \infty \}.\)

Note que nos exemplos (i) e (ii), \(\Omega\) é um conjunto no máximo enumerável, quando isso acontece dizemos que \(\Omega\) é um espaço amostral discreto. No entanto, no exemplo (iii) temos um conjunto infinito não-enumerável, nesse caso dizemos que \(\Omega\) é um espaço amostral contínuo.

1.2 Eventos

Definição 1.3 (Evento) Informalmente, um evento é qualquer subconjunto \(A\subset \Omega\).

1.2.1 Relaçoes e operações entre eventos

• Seja \(A\) um evento. Se \(\omega\) é um elemento em \(\Omega\), tal que \(\omega \in A\), dizemos que \(A\) ocorre.
• Se \(A=\{\omega\}\) para algum \(\omega \in \Omega\), dizemos que \(A\) é um evento elementar.
• Dados dois eventos \(A\) e \(B\), dizemos que \(A\subset B\), se \(\omega \in A\Rightarrow \omega \in B\). Em palavras a ocorrência de \(A\) implica a ocorrência de \(B\).
• A união de dois eventos \(A\) e \(B\) é \(A \cup B =\{\omega: \omega \in A \text{ ou } \omega \in B \}\) e representa o evento A intersecção de dois eventos \(A\) e \(B\) é \(A\cap B =\{\omega: \omega \in A \text{ e } \omega \in B\}\) e representa o evento de que ambos \(A\) e \(B\) ocorrem.
• A diferença de dois eventos \(A\) e \(B\) é \(A\setminus B = \{\omega: \omega \in A \text{ e } \omega \notin B\}\) e representa o evento de que \(A\) ocorre e \(B\) não ocorre.
• Dois eventos \(A\) e \(B\) são disjuntos ou mutuamente exclusivos se \(A\cap B =\emptyset\). Isso significa que \(A\) e \(B\) não ocorrem simultaneamente.
  
• Para qualquer evento \(A\), o complementar de \(A\) é \(A^c =\{\omega: \omega \notin A\}\) e representa o evento de que \(A\) não ocorre.
• Leis de Morgan: Sejam \(A_1,A_2,\ldots,A_n\) eventos, temos que \[\begin{align} \left( \bigcup_{i=1}^n A_i\right)^c = \bigcap_{i=1}^n A_i^c, \tag{LM1} \label{LM1} \\ \left( \bigcap_{i=1}^n A_i\right)^c = \bigcup_{i=1}^n A_i^c. \label{LM2} \tag{LM2} \end{align}\]

Observação. Note que \(\eqref{LM1}\) diz que o complementar de que pelo menos um dos \(A_i\)’s ocorre é igual ao evento de que nenhum dos \(A_i\)’s ocorra. Enquanto \(\eqref{LM2}\) diz que o complementar de que todos os \(A_i\)’s ocorrem é igual ao evento de que pelo menos um dos \(A_i\)’s não ocorre.

1.3 Probabilidade

Definição 1.4 (Definição clássica) Seja \(\Omega =\{\omega_1,\ldots,\omega_N\}\) finito, e suponhamos que cada evento elementar é igualmente provável, isto é, \[ P(\omega) = \frac{1}{N}, \, \omega \in \Omega. \] Definimos a probabilidade do evento \(A\subset \Omega\) como

\[ P(A) = \frac{|A|}{|\Omega|}. \]

Definição 1.5 (Definição axiomática) Uma probabilidade é uma função \(P: \mathcal F \rightarrow \mathbb R\), em que \(\mathcal F\) é uma classe de eventos de um espaço amostral \(\Omega\), que satisfaz as seguintes condições:

1. \(P(A) \geq 0\), para todo \(A \in \mathcal F\),
2. \(P(\Omega) = 1\),
3. (Aditividade enumerável). Para qualquer sequência \(A_1,A_2,\ldots \in \mathcal F\), tais que \(A_i \cap A_j =\emptyset\), \(i\neq j\), \[\begin{align*} P\left(\bigcup_{i=1}^\infty A_i\right)= \sum_{i=1}^\infty P(A_i). \end{align*}\]

Observação. Quando \(\Omega\) é infinito não-enumerável, geralmente é impossível associar uma probabilidade bem definida a todos os subconjuntos de \(\Omega\). Para isso, definimos uma probabilidade em uma classe mais restrita de subconjuntos de \(\Omega\) (chamada de \(\sigma\)-álgebra e definida abaixo); e apenas esses subconjuntos são chamados de eventos.

Definição 1.6 (sigma-álgebra) Uma classe \(\mathcal F \subset 2^\Omega\) é uma \(\sigma\)-álgebra (em \(\Omega \neq \emptyset\)) se satisfaz as seguintes condições

1. \(\Omega \in \mathcal F\),

2. Se \(A \in \mathcal F\), então \(A^c \in \mathcal F\),

3. Se \(A_1,A_2,\ldots \in \mathcal F\), então \(\displaystyle\bigcup_{i=1}^\infty A_i \in \mathcal F\).

O trio \((\Omega,\mathcal F, P)\) é chamado de um espaço de probabilidade.

1.3.1 Propriedades de uma probabilidade

1. \(P(\emptyset) = 0\).

2. Se \(A_1,A_2,\ldots,A_n\) são eventos dois a dois disjuntos, então \[\begin{align*} P\left(\bigcup_{i=1}^n A_i \right) = \sum_{i=1}^n P(A_i) \end{align*}\]

3. \(P(A) = 1- P(A^c)\) para todo evento \(A\).

4. Para quaisquer eventos \(A\) e \(B\), \[\begin{align*} P(B) = P(A \cap B) + P(A^c \cap B) \end{align*}\]

5. Se \(A \subset B\), então \(P(A) \leq P(B)\).

6. \(P(A)\leq 1\) para todo evento \(A\).

7. Para quaisquer eventos \(A\) e \(B\), \[\begin{align*} P(A\cup B) =P(A) + P(B) - P(A\cap B). \end{align*}\]

8. Princípio da Inclusão-Exclusão \[\begin{align*} P\left(\bigcup_{i=1}^n A_i \right) &= \sum_{i=1}^n P(A_i) - \sum_{i<j} P(A_i \cap A_j)\\ &+ \sum_{i<j<k} P(A_i \cap A_j \cap A_k) - \cdots +(-1)^{n+1} P(A_1\cap \cdots \cap A_n) \end{align*}\]

9. Subaditividade finita: Para qualquer sequência finita \(A_1,A_2,\ldots, A_n\) de eventos, \[ P\left(\bigcup_{i=1}^n A_i \right) \leq \sum_{i=1}^n P(A_i). \]

10. Subaditividade enumerável: Para qualquer sequência \(A_1,A_2,\ldots\) de eventos, \[ P\left(\bigcup_{i=1}^\infty A_i \right) \leq \sum_{i=1}^\infty P(A_i). \] As propriedades (ix) e (x), são conhecidas como Desigualdades de Boole.

Prova. Para provar i. Defina \(A_1 = \Omega\), \(A_i = \emptyset\), \(i>1\), logo \(\Omega = \bigcup _{i=1}^\infty A_i\). Além disso, \[\begin{align*} 1=P(\Omega) = P(\Omega) + \sum_{i=2}^\infty P(\emptyset) \Rightarrow \sum_{i=2}^\infty P(\emptyset) = 0 \Rightarrow P(\emptyset) = 0. \end{align*}\]

2. Defina \(A_i = \emptyset\), \(i>n\), logo \(\bigcup_{i=1}^\infty A_i = \bigcup_{i=1}^n A_i\), pelo axioma (iii) em \(\ref{}\) e a propriedade 1, segue que \[\begin{align*} P\left(\bigcup_{i=1}^n A_i\right)=P\left(\bigcup_{i=1}^\infty A_i\right) = \sum_{i=1}^n P(A_i) + \sum_{i=n+1}^\infty P(\emptyset) = \sum_{i=1}^n P(A_i) \end{align*}\]

3. Note que para qualquer \(A\subset \Omega\), temos que \(\Omega= A \cup A^c\) e \(A\cap A^c = \emptyset\), logo \[\begin{align*} 1=P(\Omega)=P(A) + P(A^c) \Rightarrow P(A^c) = 1-P(A) \end{align*}\]

4. Note que \(B = (A\cap B) \cup (A^c \cap B)\) tal que \((A\cap B) \cap (A^c \cap B) = \emptyset\), logo \[\begin{align*} P(B) = P(A\cap B) + P(A^c \cap B) \end{align*}\]

5. Como \(A\subset B\), temos que \(B=(B\setminus A) \cup A\), com \((B\setminus A) \cap A = \emptyset\), logo \[\begin{align*} P(B) = P(A) + P(A\setminus B) \geq P(A). \end{align*}\]

6. Como \(A\subset \Omega\), logo \(P(A) \leq P(\Omega) = 1\).

7. Note que \(A\cup B = (A\setminus B) \cup (A \cap B) \cup (B \setminus A)\), logo \[\begin{align*} P(A\cup B) &= P(A\setminus B) + P(A \cap B) + P(B\setminus A) \\ &= [P(A\setminus B) + P(A \cap B)] + [P(B\setminus A) + P(A\cap B)] - P(A\cap B)\\ &= P(A) + P(B) - P(A\cap B). \end{align*}\]

8. Use indução em \(n\). Note que para o caso \(n=3\), temos \[\begin{align*} P(A\cup B\cup C) &= P(A) + P(B) + P(C) - P(A\cap B) - P(A\cap C) - P(B \cap C) \\ &+ P(A\cap B \cap C). \end{align*}\]

1.3.2 Calculando probabilidades

Exemplo 1.1 Um comitê de 5 pessoas deve ser selecionado de um grupo de 6 homens e 9 mulheres. Se a seleção for feita aleatoriamente, qual a probabilidade de que o comitê seja formado por 3 homens e 2 mulheres?

Solução. Como o experimento consiste em escolher 5 pessoas do total de 15, temos que \(|\Omega|= \binom{15}{5}\). Supondo que todas as \(\binom{15}{5}\) tem a mesma probabilidade e se \(A\) representa o evento de que a seleção feita seja formada por 3 homens e 2 mulheres, temos que \(|A| = \binom{6}{3} \binom{9}{2}\). Portanto, \[\begin{align*} P(A) &= \frac{|A|}{|\Omega|} \\ &= \frac{\binom{6}{3}\binom{9}{2}}{\binom{15}{5}}=\frac{240}{1001} \end{align*}\]

Exemplo 1.2 Numa mão de pôquer de cinco cartas, o full house ocorre quando alguém sai com três cartas de mesmo valor e duas outras cartas do mesmo valor (diferente do primeiro). Assim um full house é formado por uma trinca e um par. Qual a probabilidade de alguém sair com um full house?

Solução. Vamos supor que todas \(\binom{52}{5}\) possíveis seleções são equiprováveis. Note que o número de maneiras de escolher um par é \(13 \cdot \binom{4}{2}\) e uma vez escolhido o par, o número de maneiras de escolher uma trinca é \(12 \cdot \binom{4}{3}\), logo se \(A\) é o evento de sair um full house, temos que \[\begin{align*} P(A) = \frac{13\cdot 12 \cdot \binom{4}{2} \cdot \binom{4}{3}}{\binom{52}{5}} \approx 0,0014. \end{align*}\]

Exemplo 1.3 Um estudante possui 5 livros diferentes de Probabilidade, 2 livros diferentes de Estatística e 3 livros diferentes de Computação, que serão dispostos aleatoriamente em uma prateleira. Qual a probabilidade de que os livros de cada assunto fiquem juntos?

Solução. Primeiro observe que temos 10! maneiras de dispor os 10 livros na prateleira, logo para garantir que os livros de cada assunto fiquem juntos vamos formar três blocos (um por cada assunto): o primeiro bloco é formado pelos 5 livros de Probabilidade, o segundo pelos 2 livros de Estatística e o terceiro pelos 3 livros de Computação. Assim, para o primeiro bloco temos 5! maneiras de ordenar eles, para o segundo temos 2! e para o terceiro temos 3!, finalmente temos 3! maneiras de ordenar os blocos. Portanto, a probabilidade pedida é \[\begin{align*} P(\text{os livros de cada assunto fiquem juntos}) &= \frac{5!2!3!3!}{10!}\\ &=\frac{1}{420} \end{align*}\]

1.3.3 Espaço de probabilidade no caso \(\Omega\) enumerável

Suponha que \(\Omega = \{\omega_1, \omega_2,\ldots\}\) seja um conjunto enumerável e assuma que a cada \(\omega_i \in \Omega\), atribuimos um peso \(p(\omega_i)\) tal que \(\sum_{i=1}^\infty p(\omega_i) = 1\), além disso considere como família de eventos \(\mathcal F = 2^\Omega\) e para qualquer \(A \in \mathcal F\), definimos a probabilidade de \(A\) como \[ P(A) = \sum_{i: \omega_i \in A} p(\omega_i). \]

Exemplo 1.4 Suponha um jogo no qual você ganha \(k-2\) reais com probabilidade \(\left(\frac{1}{2}\right)^k\) para qualquer \(k\geq 1\) inteiro. Qual a probabilidade de você ganhar mais de dos reais ?

Solução. Neste caso o espaço amostral é dado pela quantidade de reais que você pode ganhar no jogo, ou seja, \[ \Omega = \{-1,0,1,2,\ldots\}, \] e \[ P(\{\omega\})=P(\omega) = \left(\frac{1}{2}\right)^{\omega+2}, \; \omega \in \Omega.\] Por exemplo, \(P(\{-1\}) = 1/2\) e \(P(\{0\}) = 1/4\). O evento de interesse é \(A=\{3,4,5,6,\ldots\}\). Portanto, \[\begin{align*} P(A) = \sum_{\omega = 3}^\infty P(\omega) &= \sum_{\omega=3}^\infty \left(\frac{1}{2}\right)^{\omega + 2}\\ &=\frac{1}{4} \sum_{\omega=3}^\infty \left(\frac{1}{2}\right)^{\omega} \\ &= \frac{1}{16}. \end{align*}\]

1.4 Probabilidade Condicional

Considere o experimento que consiste em lançar um dado honesto e defina os eventos \(A=\{1,2,3\}\) e \(B=\{2,4,6\}\), temos que \(P(A) = \frac{1}{2}\), essa é a probabilidade a priori de \(A\), isto é, antes que o experimento se realize. Suponha que uma vez realizado o experimento alguém nos infrome que o resultado do mesmo é um número par, ou seja que \(B\) ocorreu. Com essa nova informação, a probabilidade de \(A\) é atualizada, pois para que \(A\) aconteça o único resultado possível do experimento deve ter sido 2. O que nos leva a

\[ P(A \text{ dado } B) = \frac{|A\cap B|}{|\Omega|} = \frac{1}{3}. \]

Essa probabilidade é chamada de probabilidade a posteriori de \(A\) dado \(B\). Daqui em diante, vamos chama-la de probabilidade de \(A\) dada a ocorrência de \(B\) ou simplesmente de probabilidade de \(A\) dado \(B\). Do exemplo, podemos generalizar com a seguinte definição:

Definição 1.7 (Probabilidade condicional) Sejam \(A,B\) dois eventos em um espaço de probabilidade \((\Omega, \mathcal F, P)\), tal que \(P(B)>0\), definimos a probabilidade condicional de \(A\) dado \(B\) como \[\begin{align*} P(A|B) = \frac{P(A\cap B)}{P(B)}. \end{align*}\]

Proposição 1.1 Seja \(B\) um evento em um espaço de probabilidade \((\Omega,\mathcal F, P)\), tal que \(P(B)>0\), temos que \(P(\cdot|B)\) é uma probabilidade.

Prova. Devemos verificar os três axiomas da definição axiomática de probabilidade. Com efeito

1. \(P(A|B) \geq 0\), para qualquer evento \(A\) (trivial).

2. \(P(\Omega|B) = \frac{P(\Omega\cap B)}{P(B)} = \frac{P(B)}{P(B)} = 1\).

3. Aditividade enumerável: Sejam \(A_1, A_2,\ldots\) eventos disjuntos dois a dois, então \[\begin{align*} P\left(\bigcup_{i=1}^\infty A_i|B\right) &= \frac{P\left(\left(\bigcup_{i=1}^\infty A_i\right) \cap B\right)}{P(B)}\\ &= \frac{P\left(\bigcup_{i=1}^\infty (A_i \cap B)\right)}{P(B)} \\ &= \frac{\sum_{i=1}^\infty P(A_i\cap B)}{P(B)} \\ &= \sum_{i=1}^\infty P(A_i|B) \end{align*}\]

Proposição 1.2 (Regra da multiplicação) Se \(A_1,\ldots,A_n\) são eventos em um espaço de probabilidade \((\Omega,\mathcal F, P)\) com \(P(A_1\cap \ldots \cap A_{n-1})>0\), então \[ P(A_1 \cap A_2 \cap \ldots \cap A_n) = P(A_1)P(A_2|A_1) \cdots P(A_n|A_1 \cap \ldots \cap A_{n-1}) \]

Exemplo 1.5 Um baralho comum com 52 cartas é dividido aleatoriamente em 4 pilhas de 13 cartas cada. Qual a probabilidade de que cada pilha tenha exatamente um ás?

Solução. Defina \(A_i = \{i-\text{ ésima pilha tem exatamente um ás}\}\), logo queremos calcular \[\begin{align*} P(A_1\cap A_2 \cap A_3 \cap A_4) &= P(A_1)P(A_2|A_1)P(A_3|A_2\cap A_1)P(A_4|A_3\cap A_2 \cap A_1 ) \\ &=\frac{\binom{4}{1}\binom{48}{12}}{\binom{52}{13}} \times \frac{\binom{3}{1}\binom{36}{12}}{\binom{39}{13}} \times \frac{\binom{2}{1}\binom{24}{12}}{\binom{26}{13}} \times 1 = 0,105 \end{align*}\]

1.4.1 Fórmula da probabilidade total

Definição 1.8 (Partição) Seja \(\Omega\neq \emptyset\), uma partição de \(\Omega\) é uma sequencia finita de conjuntos (ou eventos) \(A_1,\ldots,A_n\) tais que

1. \(A_i \cap A_j = \emptyset\) para qualquer \(i\neq j\), \(i,j=1,\ldots,n\),
2. \(\displaystyle \bigcup_{i=1}^n A_i = \Omega\).

Teorema 1.1 (Fórmula da probabilidade total) Seja \(\{A_i\}_{i=1}^n\) uma partição do espaço amostral \(\Omega\), tal que \(P(A_i)>0\) para qualquer \(i=1,\ldots, n\) e \(B\) um evento qualquer, temos que \[ P(B) = \sum_{i=1}^n P(B|A_i)P(A_i). \]

Prova. Note que \(\displaystyle B = \bigcup_{i=1}^n (B\cap A_i)\) e \((B\cap A_i) \cap (B\cap A_j)\) para qualquer \(i\neq j\). Logo \[ P(B) = \sum_{i=1}^n P(B\cap A_i) = \sum_{i=1}^n P(B|A_i) P(A_i), \] onde a ultima passagem decorre da regra da multiplicação para dois eventos.

Exemplo 1.6 Durante o mês de outubro a probabilidade de chuva em um dia determinado é de 4/10. Um time de futebol ganha um jogo em um dia com chuva com probabilidade 6/10 e em um dia sem chuva com probabilidade de 4/10. Qual a probabilidade de que esse time ganhe um jogo naquele dia de outubro?

Solução. Seja \(A\): O time ganhe um jogo naquele dia de outubro e \(B\): teve chuva naquele dia de outubro, logo \[ P(A) = P(A|B)P(B) + P(A|B^c)P(B^c) = (6/10)(4/10) + (4/10)(6/10) = 24/50 \]

Exemplo 1.7 Ao responder uma questão em uma prova de múltipla escolha, um estudante sabe a resposta ou a chuta. Seja \(p\) a probabilidade de que o estudante saiba a resposta e \(1-p\) a probabilidade de que ele chute. Suponha que um estudante que chuta a resposta tem uma probabilidade de acerto de \(1/m\), onde \(m\) é o número de alternativas em cada questão de múltipla escolha. Qual a probabilidade que ele a tenha respondido corretamente?

Solução. Denote por \(A\): o estudante tenha respondido corretamente [acerta a resposta] e por \(B\): o estudante sabe a resposta, logo \[ P(A) = P(A|B)P(B) + P(A|B^c)P(B^c) = p\cdot 1 + (1-p) \cdot 1/m = p+(1-p)/m. \] Por exemplo, se \(p=1/2\) e \(m=10\), temos que \(P(A) = \frac{11}{20}\).

Exercício 1.1 Em uma cidade, os motoristas são parados pela polícia para fazer um teste sobre o teor de álcool no sangue. Suponha que a probabilidade de que um motorista detido esteja embriagado é 5% e que o teste realizado acerta o estado de embriaguez em 80% das ocasiões. Qual a probabilidade de que o teste de um motorista detido resulte positivo?

1.4.2 Fórmula de Bayes

Teorema 1.2 (Fórmula de Bayes) Seja \(\{A_i\}_{i=1}^n\) uma partição do espaço amostral \(\Omega\), tal que \(P(A_i)>0\) para qualquer \(i=1,\ldots, n\) e \(B\) um evento, temos que \[ P(A_i|B) = \frac{P(B|A_i)P(A_i)}{\sum_{i=1}^n P(B|A_i)P(A_i)} \]

Prova. Para cada \(i=1,2,\ldots,n\), temos que \[\begin{align*} P(A_i|B)&=\frac{P(A_i\cap B)}{P(B)} \\ &=\frac{P(B|A_i)P(A_i)}{\sum_{i=1}^n P(B|A_i)P(A_i)} \end{align*}\] Na primeira passagem aplicamos a definição de probabilidade condicional, na segunda passagem aplicamos, no numerador, a regra da multiplicação e no denominador o teorema da probabilidade total.

Solução. Denote por \(A\): teste resulte positivo e por \(B\): o motorista está embriagado. \[P(A) = P(A|B)P(B) + P(A|B^c)P(B^c) = (0,80)(0,05) + (0,20)(0,95) = 23/100.\]

Exemplo 1.8 Nas mesmas condições do exemplo 3, dado que o teste de um motorista resulto negativo, qual a probabilidade de que estava dirigindo com um índice alcoólico acima do permitido?

Solução. Defina \(B\): embriagado, \(B^c\): sóbrio, \(A^c\): teste negativo, \(A\): teste positivo Pelo Teorema de Bayes, temos que \[\begin{align*} P(B|A^c) &=\frac{P(A^c|B)P(B)}{P(A^c|B)P(B) + P(A^c|B^c)P(B^c)}\\ &=\frac{(0,20)(0,05)}{(0,20)(0,05)+(0,80)(0,95)} \\ &\approx 0.01 \end{align*}\] Ou seja, a probabilidade de ocorrer um falso negativo é aproximadamente de 1% .

Exemplo 1.9 (Problema de Monty Hall) O problema de Monty Hall é um jogo famoso do programa Let’s Make a Deal apresentando por Monty Hall na década dos 60. Eis o jogo:

1. Há três portas: 1, 2, e 3.
2. Detrás de uma das portas tinha um carro e nas outras duas uma cabra.
3. O jogador escolhia uma porta, se o carro estava na porta escolhida pelo jogador então ganhava o carro.
4. Depois do jogador escolher a porta, Monty abria uma porta (diferente da escolhida pelo jogador) e sempre revelava uma cabra.

Uma vez revelada a cabra, Monty perguntava para o jogador se queria mudar para a porta ainda fechada ou ficar com a escolhida inicialmente. O que o jogador deveria fazer?

Solução. A resposta é que o jogador deveria mudar de porta se ele quer duplicar a probabilidade de ganhar o carro. Para entender isso, usaremos o Teorema de Bayes. Sem perda de generalidade vamos assumir que o jogador escolhe a porta 1 e que o Monty abre a porta 2 revelando uma cabra (lembre que ele sempre revela uma cabra).

Seja \(A_i\): o carro está na i- ésima porta, \(i=1,2,3\) e \(B\): Monty abre a porta 2. Logo, \[\begin{align*} P(A_1)=P(A_2)=P(A_3)=1/3. \end{align*}\] Atualizando as probabilidades pelo Teorema de Bayes: \[\begin{align*} P(A_1|B) &\propto P(B|A_1)P(A_1) = 1/2 \times 1/3 = 1/6.\\ P(A_2|B) &\propto P(B|A_2)P(A_2) = 0 \times 1/3 = 0.\\ P(A_3|B) &\propto P(B|A_3)P(A_3) = 1 \times 1/3 = 1/3.\\ \end{align*}\] Logo: \(P(B) = \sum_{i=1}^3 P(B|A_i)P(A_i)= 1/2\). Portanto, \(P(A_1|B) = 1/3\) e \(P(A_3|B) = 2/3\).

1.5 Independência

Definição 1.9 Sejam \(A,B\) dois eventos em um espaço de probabilidade \((\Omega, \mathcal F, P)\) dizemos que \(A\) e \(B\) são independentes se \[ P(A \cap B) = P(A) P(B). \]

Observação. Eventos disjuntos não são necessariamente independentes, a menos que um deles tenha probabilidade igual a 0. Considere, por exemplo, \(\Omega = \{1,2,3,4,5,6\}\) e os eventos \(A = \{\2,4,6\}\) e \(B=\{1,3,5\}\), claramente, \[ 0=P(A\cap B) = P(\emptyset) \neq P(A)P(B) = 1/4. \]

Definição 1.10 Sejam \(A_1,A_2,\ldots, A_n\) eventos em um espaço de probabilidade \((\Omega, \mathcal F, P)\) dizemos que \(A_1,A_2,\ldots, A_n\) são independentes se para qualquer \(k=2,\ldots,n\) \[ P(A_{i_1}\cap A_{i_2} \cap \ldots \cap A_{i_n}) = P(A_{i_1})P(A_{i_2}) \cdots P(A_{i_k}) \]

Exemplo 1.10 Considere um sistema em paralelo formado por 6 componentes como o mostrado na figura abaixo. Suponha que cada um dos componentes funciona de maneira independente com probabilidade \(p\). Qual a probabilidade que o sistema funcione?

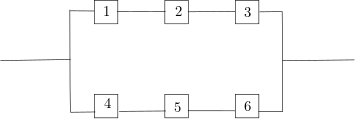
Solução. Note que o sistema é formado por dois subsistemas com três componentes cada. Para que o sistema funcione pelo menos um desses dois subsistemas deve funcionar, ou seja, o sistema não funciona se os dois subsistemas não funcionam, logo, pela independência temos que \[\begin{align*} P(\text{sistema funciona}) &= 1 - P(\text{sistema não funciona})\\ &=1-[1-p^3]^2. \end{align*}\]