Capítulo 7 Modelos de distribuições contínuas
7.1 Distribuição uniforme contínua
Definição 7.1 Dizemos que a variável aleatória \(X\) tem distribuição uniforme contínua no intervalo \([a,b]\), se sua função de densidade é \[ f(x) = \begin{cases} \frac{1}{b-a} & a \leq x \leq b, \\ 0, & \text{caso contrário} \end{cases} \] Notação: \(X\sim\) Uniforme Contínua(\([a,b]\))

A função de distribuição de uma variável uniforme contínua no intervalo \([a,b]\) é
\[ F(x) = \begin{cases} 0, & x<a\\ \frac{x-a}{b-a}, & a\leq x \leq b\\ 1, & x \geq b \end{cases} \]
Proposição 7.1 Se \(X \sim\) Uniforme Contínua(\([a,b]\)), então \[ E(X) = \frac{a+b}{2} \text{ e } Var(X) = \frac{(b-a)^2}{12} \]
Exemplo 7.1 A eficiência \(X\) de um certo componente eletrico é modelada por uma variável aleatória contínua com distribuição uniforme no intervalo \([0,100]\). Qual a probabilidade de que \(X\)
esteja entre 60 e 80 unidades
seja menor que 90 unidades
Solução. Seja \(X\): eficiencia do componente eletrico
\(P(60 \leq X \leq 80) = F(80) - F(60) = 0,20\).
\(P(X\leq 90) = F(90)=0,90.\)
7.2 Distribuição exponencial
Definição 7.2 Dizemos que a variável aleatória \(X\) tem distribuição exponencial de parâmetro \(\lambda > 0\) se, sua função de densidade é \[ f(x) = \begin{cases} \lambda e^{-\lambda x} & x \geq 0 \\ 0, & \text{caso contrário} \end{cases} \] Notação: \(X\sim\) Exponencial(\(\lambda\)).

A função de distribuição de uma variável exponencial de parâmetro \(\lambda\) é
\[\begin{align*} F(x) = \begin{cases} 1-e^{-\lambda x}, & x \geq 0 \\ 0, & \text{caso contrário} \end{cases} \end{align*}\]
Proposição 7.2 Se \(X \sim\) Exponencial(\(\lambda\)), então \[ E(X) = \frac{1}{\lambda} \text{ e } Var(X) = \frac{1}{\lambda^2} \]
Exemplo 7.2 O tempo de atendimento, em minutos, a um cliente em um serviço de informação de uma biblioteca é uma variável aleatória contínua com distribuição exponencial, com um tempo médio de atendimendo de 5 minutos. Qual a probabilidade de que o atendimento a um cliente dure mais de 10 minutos ?
Solução. Seja \(X\): Tempo de atendimento, em minutos, a um cliente em um serviço de informação de uma biblioteca \(\sim\) Exponencial(\(\lambda = 1/5\)).
\[ P(X > 10) = 1- P(X\leq 10) = 1-F(10) = e^{-10/5} = 0,1353.\]
7.3 Distribuição normal
A distribuição normal é a distribuição contínua utilizada com mais frequência nas aplicações da teoria da probabilidade. Ela constitui a base para o desenvolvimento de muitos dos métodos da Estatística.
Definição 7.3 Dizemos que a variável aleatória \(X\) tem uma distribuição normal de parâmetros \(\mu \in \mathbb R\) e \(\sigma^2>0\), se sua função de densidade é \[ f(x) = \frac{1}{\sqrt{2\pi} \sigma} e^{-(x-\mu)^2/2\sigma^2}, \; x \in \mathbb R. \] Notação: \(X\sim\) N(\(\mu\),\(\sigma^2\)).
A distribuição normal também é conhecida como a distribuição de Laplace-Gauss. No seguinte gráfico apresentamos várias curvas da normal para diferentes valores dos parâmetros \(\mu\) e \(\sigma^2\).
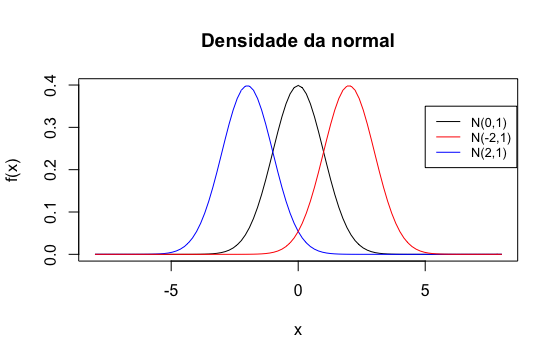
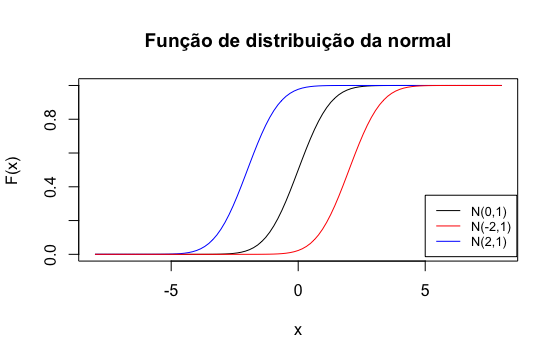
A função de distribuição da normal é
\[ F(x) = \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^x e^{-(t-\mu)^2/2\sigma^2} dt, \; x\in \mathbb R. \]
7.3.1 Propriedades da distribuição normal
A densidade \(f\) é simétrica em torno de \(\mu\), isto é: \(f(\mu+ x) = f(\mu - x)\) para qualquer \(x\in \mathbb R\).
Para qualquer \(x\in\mathbb R\), \(F(\mu + x) + F(\mu-x) = 1\).
\(x=\mu\) é o único ponto de máximos de \(f\), e o valor máximo é \(\frac{1}{\sigma \sqrt{2\pi}}\).
\(f\) tem dois pontos de inflexão: \(x=\mu - \sigma\) e \(x=\mu + \sigma\).
\(\lim_{x\to \pm \infty} f(x) = 0\).
O desvio padrão \(\sigma\) determina a largura da curva da normal: quanto maior \(\sigma\) tem-se uma curva mais larga e achatada, dito de ooutra maneira, quanto maior \(\sigma\) menos concentrada perto de \(\mu\) a densidade é (veja a figura a continuação).
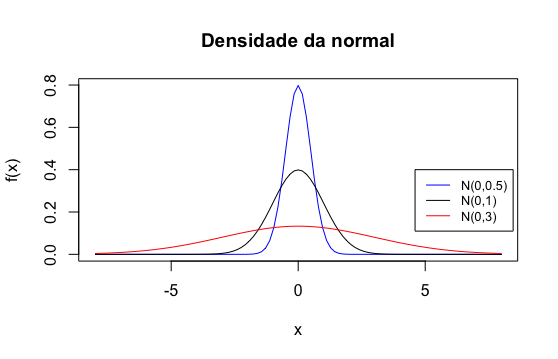
7.3.2 A distribuição normal padrão
A distribuição normal padrão resulta quando os parâmetros de uma distribuição normal correspondem a \(\mu = 0\) e \(\sigma^2 = 1\). Ou seja, dizemos que a variável \(Z\sim\) N(0,1) se sua função de densidade é
\[ \phi(z) = \frac{1}{\sqrt{2\pi}} e^{-z^2/2}, \; z\in \mathbb R. \]
A função de distribuição de uma normal padrão é denotada pela letra grega \(\Phi\) maiúscula e é dada por
\[ \Phi(z) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^z e^{-t^2/2} dt, \; x\in\mathbb R. \]
Observação. Os valores de \(\Phi(z)\) não são possíveis de obter analiticamente, no entanto, podem ser aproximados numericamente e encontram-se tabelados para os valores de \(z\geq 0\). Note que se \(z<0\), podemos calcular \(\Phi(z)\) através de \(\Phi(z) = 1-\Phi(-z)\).
A continuação apresentamos alguns resultados úteis para o cálculo de probabilidades envolvendo uma distribuição normal.
Proposição 7.3 Seja \(X\) uma variável aleatória com média \(\mu\) e variância \(0<\sigma^2<\infty\). Se \[ Z = \frac{X-\mu}{\sigma}, \] então \(E(Z) = 0\) e \(Var(Z)=1\).
Proposição 7.4 Seja \(X\sim\) N(\(\mu,\sigma^2\)), e defina \(Y=aX + b\), então \(Y\sim\) N(\(a\mu + b\), \(a^2 \sigma^2\)).
Prova. \[\begin{align*} F_Y(y) &= P(Y \leq y) \\ &= P(aX + b \leq y) \\ &=P\left(X\leq\frac{y-b}{a}\right)\\ &=F_X\left(\frac{y-b}{a}\right) \end{align*}\] Logo, \[\begin{align*} f_Y(y) &= F_Y'(y)\\ &=\frac{1}{a} F_X'\left(\frac{y-b}{a}\right) \\ &=\frac{1}{a}f_X\left(\frac{y-b}{a}\right)\\ &=\frac{1}{\sqrt{2\pi} (a\sigma)} e^{-(y-(a\mu + b))^2/2(a^2\sigma^2)} \end{align*}\]
Corolário 7.1 Seja \(X\sim\) N(\(\mu,\sigma^2\)), então \(Z=\frac{X-\mu}{\sigma}\sim\) N(0,1).
Corolário 7.2 Seja \(Z\sim\) N(0,1), então \(X = \sigma Z + \mu \sim\) N(\(\mu,\sigma^2\))
Proposição 7.5 Se \(X\sim\) N(\(\mu,\sigma^2\)), então \[ E(X) = \mu \text{ e } Var(X) = \sigma^2. \]
Prova. Podemos escrever \(X = \sigma Z + \mu\), onde \(Z\sim N(0,1)\), logo \(E(X) = \sigma E(Z) + \mu = \mu\) e \(Var(X)=\sigma^2 Var(Z) = \sigma^2\).
7.3.3 Calculando probabilidades de uma \(N(\mu,\sigma^2)\) a partir da \(N(0,1)\)
Seja \(F\) a função de distribuição de uma variável aleatória normal com média \(\mu\) e variância \(\sigma^2\), e \(\Phi\) a função de distribuição de uma normal padrão, para qualquer \(a\in \mathbb R\), tem-se que
\[ F(a)=P(X\leq a) = P\left(Z \leq \frac{a-\mu}{\sigma}\right) = \Phi\left(\frac{a-\mu}{\sigma}\right). \]
Exemplo 7.3 Suponha que os diâmetros das bolas de golf produzidas por uma companhia seguem uma distribuição normal com \(\mu = 1,96\) polegadas e \(\sigma = 0,04\) polegadas. Uma bola de golf é considerada defeituosa se seu diâmetro é menor que 1,90 polegadas ou maior que 2,02 polegadas. Qual a porcentagem de bolas de golf defeituosas fabricadas pela companhia?
Solução. Seja \(X\): Diâmetro de uma bola de golf fabricada pela companhia. Logo, \[\begin{align*} P(X < 1,90 \text{ ou } X> 2,02) &= 1- P(1,90 \leq X \leq 2,02) \\ &=1-[F(2,02)-F(1,90)]\\ &=1-\left[\Phi\left(\frac{2,02 -1,96}{0,04}\right) -\Phi\left(\frac{1,90 -1,96}{0,04}\right)\right]\\ &=1-[\Phi(1,5)-\Phi(-1,5)]\\ &=2-2\Phi(1,5)\\ &=2-2(0,9331)=0,1336 \end{align*}\]
7.4 Quantis da distribuição normal
Seja \(X\) uma variável aleatória contínua com função de distribuição \(F\) e seja \(p\in(0,1)\), definimos o \(p\)-ésimo quantil como o valor \(Q(p)\) tal que \(F(Q(p)) = p\).
No caso de \(X \sim\) \(N(\mu,\sigma^2)\), temos que
\[\begin{align*} F(Q(p)) = \Phi\left(\frac{Q(p) - \mu}{\sigma}\right) = p. \end{align*}\]
Note que devemos encontrar o \(p\)-ésimo quantil da normal padrão, denotado por \(z(p)\) e logo \(Q(p)\) será o valor tal que \(z(p) = \frac{Q(p) - \mu}{\sigma}\), isto é, \(Q(p) = \mu + \sigma z(p)\).
Por exemplo, se \(p=0,05\), queremos achar o valor \(z(p)\) tal que \(\Phi(z(p)) = p = 0,05\), Neste caso, procurando na tabela da normal, temos que \(z(0,05)=-1.64\) e \(Q(0.05) = \mu + 0,05 \sigma\). Veja a figura a seguir:
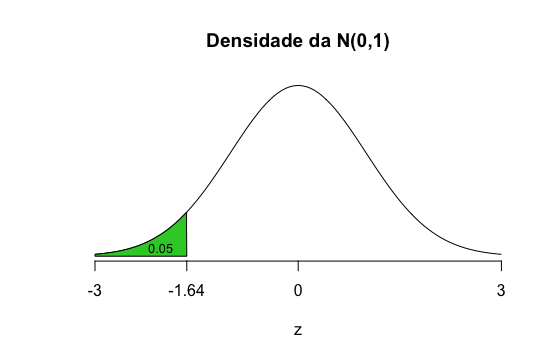
Em Inferência Estatística, os quantis de uma distribuição normal padrão recebem o nome de valores críticos e frequentemente é usada a notação: \(z_\alpha= z(1-\alpha), \; \alpha \in (0,1)\) e eles tem um papel fundamental na definição de intervalos de confiança e a região crítica de testes de hipóteses.
Exemplo 7.4 Numa população o nível sérico de colesterol em adultos (medido em mg/dl) é uma variável aleatória com distribuição normal com parâmetros \(\mu=225\) e \(\sigma=75\). Calcule o valor acima do qual se encontra o colesterol de 10% da população que tem os níveis mais elevados.
Solução. Seja \(X\): Nível de colesterol de uma pessoa selecionada aleatoriamente dessa população \(\sim\) N(225,\(75^2\)), logo \[ Z = \frac{X - 225}{75} \sim \text{N(0,1)}. \] Queremos achar valor \(a\) tal que \(P(X > a) = 0.10 \iff P(X \leq a)=0.90\), ou seja, \(a=Q(0.90)\). Logo, \(a=\mu + \sigma z(0.90)= 225 + 75 \times 1,28 = 321\).
Portanto, 10% da população tem um nível de colesterol acima de 321 mg/dl.
7.5 Aproximação normal à binomial
Lembre que uma variável aleatória \(X\) tem distribuição binomial com parâmetros \(n\) e \(p\) se sua função de probabilidade é dada por
\[ p(x) = \binom{n}{x} p^x (1-p)^{n-x}, \; x=0,1,\ldots, n. \]
Quando \(n\) é muito grande por veces resulta inviável calcular a probabilidade de que \(X\) assuma um certo conjunto de valores. Consideremos o seguinte exemplo:
Exemplo 7.5 Durante um longo período tem se determinado que 70% dos advogados que apresentam o exame da OAB são aprovados. Suponha que 500 advogados que apresentam o exame, qual a probabilidade de que pelo menos 370 deles sejam aprovados.
Seja \(X\): Número de advogados que aprovam o exame dentre os 500 \(\sim\) Binomial(500,0.70). \[ P(X \geq 370) = \sum_{x=370}^{500} \binom{500}{x} (0.70)^x (0.30)^{500-x} \] Nesse caso teriamos que calcular 131 probabilidades binomiais, o que resulta uma tarefa bastante tediosa se tivessemos que usar uma calculadora ou pior se tivessemos que realizar o cálculo “à mão”.
Diante dessa situação podemos usar a distribuição normal para aproximar probabilidades binomiais. O seguinte teorema mostra como isso pode ser feito.
Teorema 7.1 Seja \(X\sim\) Binomial(\(n,p\)). Se \(n\) é suficientemente grande, então para \(x=0,1,\ldots,n\)
\[\begin{align*} P(X \leq x) = P(X \leq x+0,5) &\approx \Phi\left( \frac{x + 0,5 - np}{\sqrt{np(1-p)}} \right) \\ P(x \leq X \leq y) = P(x - 0,5\leq X \leq y+0,5) &\approx \Phi\left(\frac{ y + 0,5 - np}{\sqrt{np(1-p)}}\right) - \Phi\left(\frac{ x - 0,5 - np}{\sqrt{np(1-p)}}\right) \end{align*}\]
Observação. O procedimento de substrair e somar 0,5 é conhecido como correção de continuidade de Fisher e fornece uma aproximação mais precisa, especialmente quando \(n\) não for muito grande.
Dois critérios que oferecem uma boa aproximação comumente usados são: \(np\geq 5\) e \(n(1-p) \geq 5\) ou \(np(1-p)\geq 10\).
A continuação apresentamos a função de probabilidade de uma distribuição binomial e a densidade da distribuição normal para diferentes valores de \(n\) e \(p\).
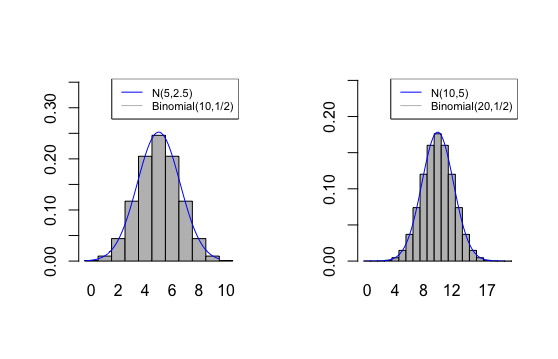
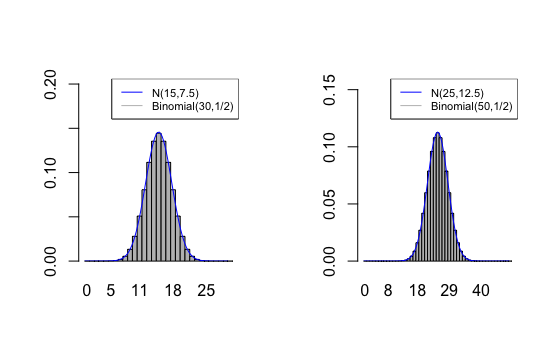
Agora, usaremos o Teorema 9.1. para responder ao Exemplo 9.4. Nesse caso \(\mu = 500\times 0.70 = 350\) e \(\sigma^2 = 500 \times 0.70 \times 0.30 = 105\)
\[\begin{align*} P(X\geq 370) &= 1 - P(X \leq 369) \\ &=1-\Phi\left( \frac{369 +0,5 - 350}{\sqrt{105}} \right)\\ &=1-\Phi(1.90)\\ &=1-0,9713\\ &=0.0287. \end{align*}\] Portanto, a probabilidade de pelo menos 370 advogados aprovem o exame da OAB é aproximadamente de 2%.
Exemplo 7.6 Um fabricante sabe por experiência que o 4% de um lote contendo um certo produto é rejeitado por defeitos. Se um novo lote de 800 unidades vai ser inspecionado. Qual a probabilidade aproximada de que menos de 35 unidades sejam rejeitadas?
Solução. Seja \(X\): Número de produtos rejeitados por defeito \(\sim\) Binomial(800,0,04), podemos usar a distribuição normal com \(\mu = 800 \times 0,04 = 32\) e \(\sigma^2 = 800 \times 0,04 \times 0,96 = 30,72\). Logo, \[ P(X<35) = P(X\leq 34) = \Phi\left( \frac{34+0,5 - 32}{\sqrt{30,72}}\right) = \Phi(0,45)=0,6736. \]
Exemplo 7.7 O tamanho ideal de uma turma de primeiro ano em uma faculdade particular é de 150 alunos. A faculdade, sabendo de experiências anteriores que, em média, apenas 30% dos alunos aceitos vão de fato seguir o curso, usa a prática de aprovar os pedidos de matrícula de 450 estudantes. Calcule a probabilidade de que mais de 150 estudantes de primeiro ano frequente as aulas nesta faculdade.
Solução. Seja \(X\): Número de estudantes que seguem o curso, então \(X\) é uma variável binomial com distribuição binomial com parâmetros \(n=450\) e \(p=0,3\). Usando a aproximação normal à binomial, temos que
\[\begin{align*} P(X\geq 150) &\approx 1-\Phi\left( \frac{150 + 0,5 - (450)(0,3)}{\sqrt{(450)(0,3)(0,7)}} \right) \\ &=1-\Phi(1,59) \\ \approx 0,0559. \end{align*}\] Portanto, menos do 6% das vezes mais que 150 dos 450 estudantes aceitos vão de fato seguir o curso.
7.6 A curtose e a distribuição normal
A curtose é uma medida de forma que mostra o achatamento da curva da função de densidade de probabilidade de uma variável aleatória.
Definição 7.4 Tomando a distribuição normal como referência, diremos que uma distribuição pode ser menos “achatada” que a normal (LEPTOCÚRTICA) ou mais “achatada” que a normal (PLATICÚRTICA). A distribuição normal desde o ponto de vista da curtose, é chamada de MESOCÚRTICA.
Definição 7.5 Seja \(X\) uma variável aleatória (discreta ou contínua) com média \(\mu\) e variância \(\sigma^2\). Então, o coeficiente de curtose de \(X\) é definida como
\[ \kappa = \frac{E[(X-\mu)^4]}{\sigma^4} - 3 \]
Critério
Se \(\kappa < 0\), então a distribuição de \(X\) é leptocúrtica.
Se \(\kappa = 0\), então a distribuição de \(X\) é mesocúrtica.
Se \(\kappa > 0\), então a distribuição de \(X\) é platicúrtica.
7.7 Distribuição Gama
Definição 7.6 A função Gama de Euler \(\Gamma: (0,\infty) \rightarrow \mathbb R\) é definida por \[ \Gamma(\alpha) = \int_{0}^\infty x^{\alpha-1} e^{-x} dx, \] e possui as seguintes propriedades:
\(\Gamma(\alpha + 1)= \alpha \Gamma(\alpha)\), \(\alpha >0\).
\(\Gamma(n+1) = n!\) para \(n\geq 0\) inteiro.
Definição 7.7 Dizemos que uma variável aleatória \(X\) tem distribuição gama com parâmetros \(\alpha >0\) e \(\lambda>0\) se, sua função de densidade é \[ f(x) = \begin{cases} \frac{\lambda^\alpha}{\Gamma(\alpha)} x^{\alpha -1} e^{-\lambda x}, & x >0 \\ 0, & \text{caso contrário} \end{cases} \] Notação: \(X \sim\) Gama(\(\alpha,\lambda\))
O parâmetro \(\alpha\) é um parâmetro de forma, ao passo que o parâmetro \(\lambda\) é um parâmetro de escala, podemos reparametrizar essa distribuição introduzindo a mudança \(\theta = 1/\lambda\), neste caso \(\theta\) é chamado de taxa da distribuição.
A continução apresentamos várias curvas da densidade da gama para diferentes valores de \(\alpha\) e \(\lambda\).
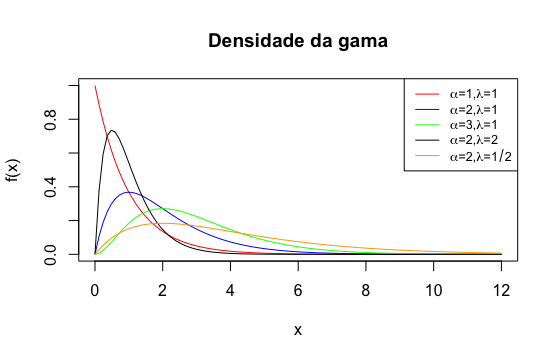
Como \(f\) é uma função de densidade, temos que: \[ \int_{0}^\infty x^{\alpha - 1}e^{-\lambda x} dx = \frac{\Gamma(\alpha)}{\lambda^\alpha}, \; \alpha, \lambda > 0. \]
Além disso,
- Se \(\lambda = 1\), a distribuição é chamada de gama padrão e, sua função de densidade é dada por
\[ f_1(x;\alpha) = \frac{1}{\Gamma(\alpha)} x^{\alpha-1} e^{-x}, \; x>0 \]
- Se \(\alpha=1\), então Gama(\(1,\lambda\)) \(\equiv\) Exponencial(\(\lambda\)).
A função de distribuição de uma gama padrão é definida por
\[ F_1(x;\alpha) = \int_0^x \frac{1}{\Gamma(\alpha)} x^{\alpha-1} e^{-x}, \; x>0, \] e recebe o nome de função gama incompleta.
Proposição 7.6 Seja \(X\sim\) Gama(\(\alpha,\lambda\)), então
\[ F_X(x) = F_1(\lambda x;\alpha) \]
Prova. Seja \(x>0\), logo \[\begin{align*} \frac{d}{dx} F_1(\lambda x;\alpha) &= \lambda f_1(\lambda x;\alpha) \\ &=\frac{\lambda^\alpha}{\Gamma(\alpha)} x^{\alpha-1} e^{-\lambda x}\\ &=f_X(x) \end{align*}\] Portanto, \(F_1(\lambda x;\alpha) = F_X(x)\).
Proposição 7.7 Seja \(X\sim\) Gama(\(\alpha,\lambda\)), então: \[E(X) =\frac{\alpha}{\lambda} \text{ e } Var(X) = \frac{\alpha}{\lambda^2}\]
Exemplo 7.8 Suponha que o tempo de sobrevivência de um rato macho em semanas exposto a 240 rads de radiação gamma tem uma uma distribuição gama com \(\alpha = 8\) e \(\lambda = 1/15\). Determine
a probabilidade de que um rato sobreviva entre 60 e 120 semanas.
a probabilidade de que um rato sobreviva pelo menos 30 semanas.
o tempo médio de sobrevivência de um rato.
Solução. Seja \(X\): Tempo de sobrevivência de um rato, em semanas, exposto a 240 rads de radiação gamma \(\sim\) Gama(\(\alpha=8\),\(\lambda=1/15\)). Logo
Queremos calcular \(P(60 \leq X \leq 120)\). Com efeito, \[\begin{align*} P(60 \leq X \leq 120) &= F_X(120)- F_X(60) \\ &=F_1\left(\frac{120}{15};8\right) - F_1\left(\frac{30}{15};8\right) \\ &=F_1(8;8)-F_1(4;8) = 0,547 - 0,051 = 0,496. \end{align*}\]
\(P(X \geq 30) = 1-F_X(30)=1 - F_1\left(\frac{30}{15};8\right) = 1 - F(2) = 1- 0,001 = 0,999\)
\(E(X) = \frac{\alpha}{\lambda} = (8)(15) = 120\) semanas.
7.8 Distribuição qui-quadrada
Definição 7.8 Dizemos que uma variável aleatória \(X\) tem distribuição qui-quadrada com \(\nu\) graus de liberdade se, sua função de densidade é \[ f(x) = \begin{cases} \frac{1}{2^{\nu/2}\Gamma(\nu/2)} x^{(\nu/2)-1}e^{-x/2}, x>0 \\ 0, \text{caso contrário} \end{cases} \]
Observação. Note que, se \(\alpha = \nu/2\) e \(\lambda = 1/2\), então Gama(\(\nu/2,1/2\)) \(\equiv\) \(\chi^2_{\nu}\).
A figura abaixo mostra diferentes curvas da função de densidade de uma qui-quadrado para diferentes valores de \(\nu\).
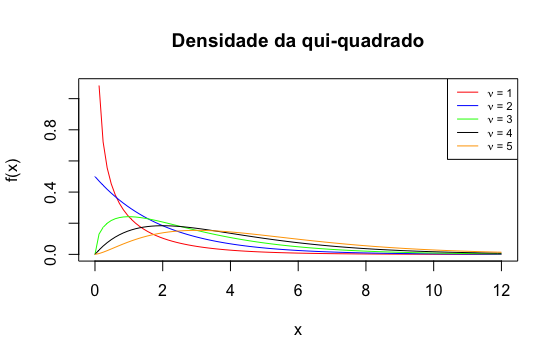
7.9 Distribuição t-Student
Definição 7.9 Dizemos que uma variável aleatória \(X\) tem distribuição \(t\)-Student com \(\nu\) graus de liberdade se, sua função de densidade é
\[ f(x) = \frac{\Gamma(\frac{\nu + 1}{2})}{\sqrt{\nu \pi}\Gamma(\nu/2)} \frac{1}{(1+x^2/\nu)^{(\nu + 1)/2}}, \; x \in \mathbb R. \]
A figura abaixo mostra diferentes curvas da função de densidade de uma t-Student para diferentes valores de \(\nu\). Além disso, adicionamos uma normal padrão, note que a distribução t-Student é uma distribuição com “caudas mais pesadas” que a normal.

As distribuições qui-quadrado e t-Student estão relacionadas com a distribuição normal como segue:
Se \(Z_1,\ldots,Z_n\) são variáveis aleatórias independentes e identicamente distrbibuídas com distribuição normal padrão, então a variável \(Y = \sum_{i=1}^n Z_i^2\) tem distribuição qui-quadrado com n graus de liberdade.
Se \(Z\) e \(Y\) são variáveis aleatórias independentes, \(Z\sim N(0,1)\) e \(Y\sim \chi^2_{\nu}\), então a variável \[ T = \frac{Z}{\sqrt{Y/\nu}},\] tem distribuição t de Student com n graus de liberdade
7.9.1 Amostragem de uma população normal
Definição 7.10 Seja \(F\) uma distribuição de probabilidade. Uma amostra aleatória de tamanho \(n\) de uma população \(F\) é uma sequência finita \(X_1,X_2,\ldots, X_n\) de variáveis aleatórias independentes e identicamente distribuídas com distribuição \(F\).
Nesta seção lidamos com amostras obtidas a partir de uma população normal. A amostragem oriundas de populações normais conduz a diversas propriedades úteis da amostragem estatística e também a muitas distribuições amostrais amplamente conhecidas.
Proposição 7.8 Seja \(X_1, X_2, \ldots, X_n\) uma amostra aleatória de uma população normal com média \(\mu\) e variância \(\sigma^2\), defina, \(\bar X = \frac{X_1 + \ldots + X_n}{n}\) e \(S^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \bar X)^2\) como média amostral e variância amostral de \(X_1,\ldots, X_n\), respectivamente. Então \(\bar X\) e \(S^2\) são independentes, com
\(\bar X \sim N(\mu,\sigma^2/n)\)
\(\frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1}\)
\(\frac{\sqrt{n}(\bar X -\mu)}{S} \sim t_{n-1}\)
7.10 Distribuição de Cauchy-Lorentz
Definição 7.11 Dizemos que uma variável aleatória \(X\) tem distribuição de Cauchy (ou Cauchy-Lorentz) com parâmetros \(\alpha \in \mathbb R\) e \(\beta > 0\) se, sua função de densidade é \[ f(x)=\frac{1}{\pi \beta \{1+[(x-\alpha)/\beta]^2\}}, \; x\in\mathbb R \]
A seguir apresentamos várias curvas da densidade da Cauchy para diferentes valores de \(\alpha\) e \(\beta\).
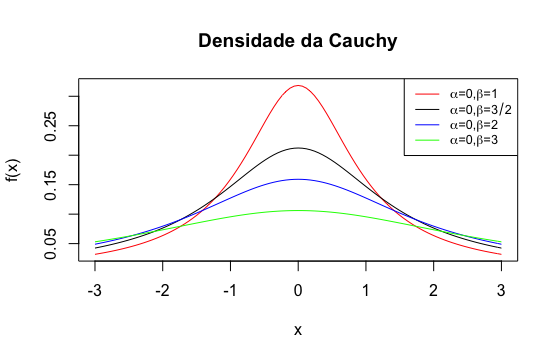
Observação. Quando \(\alpha=0\) e \(\beta = 1\), temos a distribuição Cauchy padrão, cuja função de densidade é
\[ f(x) = \frac{1}{\pi (1+x^2)}, \; x\in\mathbb R \]
É possível mostrar que a média da distribuição de Cauchy não existe. De fato, se tentamos calcular a média de \(X\sim\) Cauchy(0,1), temos que para qualquer \(t\in\mathbb R\):
\[\begin{align*} E(X) &= \int_{-\infty}^\infty \frac{x}{\pi (1+x^2)} dx\\ &= \int_{-\infty}^t \frac{x}{\pi (1+x^2)} dx + \int_{t}^\infty \frac{x}{\pi (1+x^2)} dx \\ &= \frac{1}{\pi}\left[\int_{-\infty}^{1+t^2} \frac{du}{u} + \int_{1+t^2}^{\infty} \frac{du}{u} \right] \\ &= \frac{1}{\pi}\left[ \ln(1+t^2) - \ln(-\infty) + \ln(\infty) - \ln(1+t^2) \right] \\ &=\infty - \infty \; (\text{não definido}) \end{align*}\] Portanto, \(E(X)\) não existe.
Observação. De fato \(E(|X|) = \infty\), portanto não existem os momentos \(E(X^n)\) para qualquer \(n\geq 1\). Em particular, a função geradora de momentos não existe.
A pesar de não existir a média da distribuição de Cauchy é possível mostrar, por exemplo, que a médiana é \(\tilde \mu = \alpha\). Para simplificar os cálculos assuma que \(X\sim\) Cauchy(0,1), mostraremos que \(\tilde \mu = 0\):
\[\begin{align*} F(0)=P(X\leq 0) &= \frac{1}{\pi}\int_{-\infty}^0 \frac{dx}{1+x^2}\\ &=\frac{1}{\pi} \left[\mathrm{arctg}(x)\right]_{-\infty}^0\\ &=\frac{1}{\pi} (0-(-\pi/2)) = 1/2. \end{align*}\]
Portanto, \(\tilde \mu = 0\).
Exemplo 7.9 Mostraremos nesse exemplo como a distribuição de Cauchy descreve a distância horizontal à qual um segmento de linha inclinado a um ângulo aleatório com distribuição uniforme contínua em [\(-\pi/2, \pi/2\)] corta o eixo \(x\). A situação é apresentada na figura abaixo.
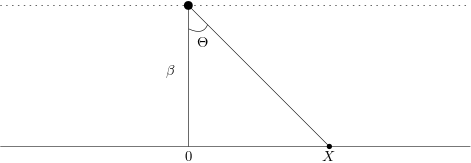
Solução. Seja \(\Theta\) o ângulo daquele segmento, com um ponto fixo de rotação, que faz com o eixo \(x\) (como mostrado na figura acima). Então \(\Theta \sim\) Uniforme Contínua[\(-\pi/2,\pi/2\)]. Além disso,
\[\begin{align*} F_X(x)=P(X \leq x) &= P(\mathrm{tg}(\Theta)\leq \frac{x}{\beta})\\ &=P(\Theta \leq \mathrm{arctg}(x/\beta))\\ &=F_{\Theta}(\mathrm{arctg}(x/\beta))\\ &= \frac{1}{\pi}\left[\mathrm{arctg}(x/\beta) + \pi/2\right] \end{align*}\] Logo,
\[\begin{align*} f_X(x) = \frac{d F(x)}{dx} &= \frac{1}{\pi \beta} \left(\frac{1}{1+(x/\beta)^2}\right) \end{align*}\] Portanto, \(X\sim\) Cauchy(0,\(\beta\)).
7.11 Distribuição Beta
Definição 7.12 A função \(B:(0,\infty) \times (0,\infty) \rightarrow \mathbb R\) é definida por \[ B(\alpha,\beta) = \int_0^1 x^{\alpha -1} (1-x)^{\beta - 1} dx, \]
Observação. A função beta está relacionada à função gama por meio da seguinte identidade: \(B(\alpha,\beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha + \beta)}\).
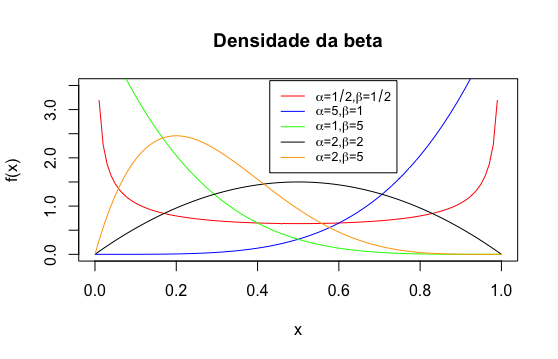
Definição 7.13 Dizemos que uma variável aleatória \(X\) tem distribuição beta com parâmetros \(\alpha>0\) e \(\beta>0\) se, sua função de densidade é
\[ f(x) = \begin{cases} \frac{1}{B(\alpha,\beta)}x^{\alpha-1} (1-x)^{\beta -1}, & x \in (0,1) \\ 0 & \text{caso contrário} \end{cases} \]
A função de distribuição de uma variável aleatória beta, em geral, recebe o nome de função beta incompleta e é dada por
\[ F(x) = \int_0^x \frac{1}{B(\alpha,\beta)} t^{\alpha - 1} (1-t)^{\beta - 1} dt. \]
Se \(\alpha\) e \(\beta\) são inteiros, então
\[\begin{align*} F(x) &= \int_0^x \frac{1}{B(\alpha,\beta)} x^{\alpha - 1} (1-x)^{\beta - 1}\\ &= \sum_{i=\alpha}^n \binom{n}{i} x^i(1-x)^{n-i}, \end{align*}\] onde \(n=\alpha+\beta-1\).
Proposição 7.9 Seja \(X\sim\) Beta(\(\alpha,\beta\)), então \[ E(X) = \frac{\alpha}{\alpha + \beta} \text{ e } Var(X) = \frac{\alpha\beta}{(\alpha + \beta)^2 (\alpha + \beta +1)} \]
Prova. Pela definição de esperança, temos
\[\begin{align*} E(X) &=\frac{1}{B(\alpha,\beta)}\int_{0}^1 x^\alpha (1-x)^{\beta -1} dx\\ &=\frac{B(\alpha+1,\beta)}{B(\alpha,\beta)}\\ &=\frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta)}\times \frac{\Gamma(\alpha+1) \Gamma(\beta)}{\Gamma(\alpha + \beta + 1)}\\ &=\frac{\alpha}{\beta}. \end{align*}\]
O cálculo da variância é deixado como exercício.
Exemplo 7.10 Um distribuidor de combustível tem tanques de armazenamento de grande capacidade com um abastecimento fixo, que são cheios cada segunda. Ele deseja saber se a porcentagem de combustível vendido durante a semana. Depois de várias semanas de observação descobre que essa porcentagem pode ser bem modelada por uma variável aleatória com distribuição beta com \(\alpha=4\) e \(\beta = 2\). Qual a probabilidade de que venda pelo menos 90% de suas existências em uma semana?
Solução. Seja \(X\): porcentagem de combustível vendido durante a semana \(\sim\) Beta(4,2).
\[\begin{align*} P(X>0.90) &= 1-\int_0^{0.90} \frac{1}{B(4,2)} t^{3} (1-t) dt\\ &=1- F(0.90)\\ &=0.08. \end{align*}\]
7.12 Distribuição Log-Normal
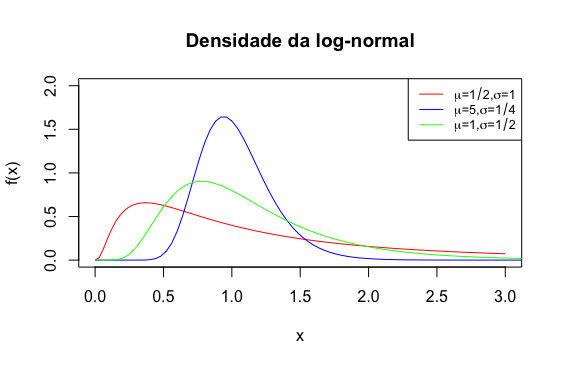
Definição 7.14 Dizemos que uma variável aleatória \(X\) tem distribuição Log-Normal com parâmetros \(\mu\in\mathbb R\) e \(\sigma^2 > 0\) se sua função de densidade é dada por:
\[ f(x) = \frac{1}{x\sigma\sqrt{2\pi}}e^{-(\ln x - \mu)^2/2\sigma^2}, \; x \geq 0. \]
Notação: \(X\sim\) Log-Normal(\(\mu,\sigma^2\)).
Observação. \(X\sim\) Log-Normal(\(\mu,\sigma^2\)) se \(Y=\ln X\sim\) N(\(\mu,\sigma^2\)) ou equivalentemente, se \(Y \sim\)N(\(\mu,\sigma^2\)), então \(X=e^Y\sim\) log-normal(\(\mu,\sigma^2\)).
A função de distribuição de \(X\) é dada por
\[\begin{align*} F(x) = P(X \leq x) &= P(\ln X \leq \ln x)\\ &=P(Y \leq \ln x)\\ &=P\left(Z\leq \frac{\ln x - \mu}{\sigma}\right)\\ &=\Phi\left(\frac{\ln x - \mu}{\sigma}\right) \end{align*}\]
Agora, se \(X\sim\) Log-Normal(\(\mu,\sigma^2\)), \(Y\sim\)N(\(\mu,\sigma^2\)) e \(Z\sim\) N(0,1), temos que
\[ E(X) = E(e^Y) = E(e^{\mu + \sigma Z}) = e^\mu E(e^{\sigma Z}) = e^\mu M_Z(\sigma) = e^{\mu + (\sigma^2t^2)/2}. \]
\[ E(X^2) = E(e^{2Y}) = E(e^{2\mu + 2\sigma Z}) = e^{2\mu} E(e^{2\sigma Z}) = e^{2\mu}M_{Z}(2\sigma) = e^{2\mu+2\sigma^2}. \]
Portanto,
\[ Var(X) = e^{2\mu+2\sigma^2} - e^{2\mu+\sigma^2}. \]
Em geral, o \(n\)-ésimo momento de \(X\sim\) log-normal(\(\mu,\sigma^2\)).
\[ E(X^n) = e^{n\mu - n^2\sigma^2/2}. \]
Observação. A função geradora de momentos da distribuição Log-Normal não existe.
Exemplo 7.11 Suponha que o preço de uma ação (em dólares) negociada na bolsa de valores segue uma distribuição Log-Normal com parâmetros \(\mu = 5\) e \(\sigma^2 = 1\). Determine:
a probabilidade de que o preço daquela ação não supere os $250.
o p-ésimo quantil do preço daquela ação.
Solução. Seja \(X\); preço da ação \(\sim\) log-normal(\(5,1\)),
P(X < 250) &= ()\ &=(0.52) .
Seja \(Q(p)\) o p-ésimo quantil de \(X\), então \[ F_X(Q(p)) = p \iff \Phi\left(\frac{\ln(x) - 5}{1}\right) = p, \] logo: \(z(p) = \ln(Q(p)) - 5 \iff Q(p) = e^{z(p) + 5}\).
Observação. Em geral, se \(X\sim\) log-normal(\(\mu,\sigma^2\)), o \(p\)-ésimo quantil de \(X\) vem dado por: \[ Q(p) = e^{\sigma z(p) + \mu}. \]
7.13 Distribuição de Pareto
Definição 7.15 Dizemos que a variável aleatória \(X\) tem distribuição de Pareto com parâmetros \(\alpha,\beta >0\), se sua função de densidade é
\[ f(x) =\begin{cases} \frac{\alpha \beta^\alpha}{x^{\alpha + 1}}, & x\geq \beta \\ 0, & x < \beta \end{cases} \]
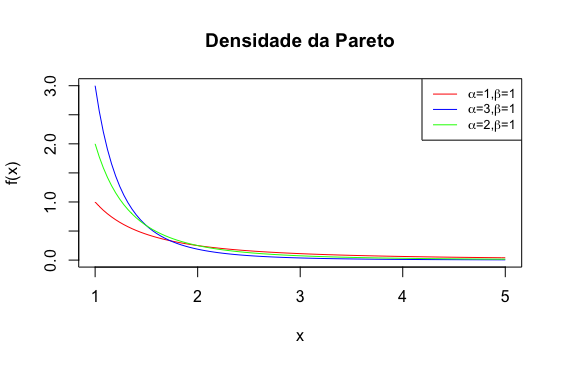
A função de distribuição de \(X\) é dada por
\[\begin{align*} F(x) &= \int_\beta^x \frac{\alpha\beta^\alpha}{t^{\alpha+1}} dt \\ &=\alpha\beta^\alpha \int_\beta^x t^{-\alpha-1} dt \\ &=\alpha \beta^\alpha \left[-\frac{t^{-\alpha}}{\alpha}\right]_\beta^x \\ &= 1 - \left(\frac{\beta}{x}\right)^\alpha, \; x \geq \beta \end{align*}\]
Em suma
\[\begin{align*} F(x) = \begin{cases} 1- \left(\frac{\beta}{x}\right)^\alpha, & x\geq \beta \\ 0 & x < \beta \end{cases} \end{align*}\]
Proposição 7.10 Seja \(X\sim\) Pareto(\(\alpha,\beta\)), então
\[ E(X) = \begin{cases} \frac{\alpha\beta}{\alpha - 1}, & \alpha > 1,\\ \infty, & \alpha \leq 1 \end{cases} \]
e
\[ Var(X) = \begin{cases} \frac{\beta^2\alpha}{(\alpha - 1)^2(\alpha - 2)}, & \alpha >2,\\ \infty & \alpha \geq 2 \end{cases} \]
Prova. \[\begin{align*} E(X) &= \int_\beta^\infty x \frac{\alpha\beta^\alpha}{x^{\alpha+1}} dx\\ &= \int_\beta^\infty \frac{\alpha\beta^\alpha}{x^\alpha} dx \\ &= \alpha\beta^\alpha \left[ - \frac{\beta^{-\alpha + 1}}{-\alpha +1}\right]_\beta^\infty = \begin{cases} \frac{\alpha\beta}{\alpha - 1}, & \alpha > 1,\\ \infty, & \alpha \leq 1 \end{cases} \end{align*}\]
\[\begin{align*} E(X^2) &= \int_\beta^\infty x \frac{\alpha\beta^\alpha}{x^{\alpha+1}} dx\\ &= \alpha\beta^\alpha\left[ \frac{x^{-\alpha + 2}}{-\alpha + 2}\right]_\beta^\infty = \begin{cases} \frac{\alpha\beta^2}{\alpha - 2}, & \alpha > 2,\\ \infty, & \alpha \leq 2 \end{cases} \end{align*}\] O resultado segue, calculando \(Var(X) = E(X^2) - [E(X)]^2\)
Exercício 7.1 Mostre que para \(n\geq 1\) \[ E(X^n) = \begin{cases} \frac{\alpha\beta^n}{\alpha - n}, & \alpha > n,\\ \infty, & \alpha \leq n \end{cases} \]
Exemplo 7.12 Suponha que a renda em reais de uma certa população tem distribuição de Pareto com parâmetro de forma \(\alpha = 3\) e parâmetro de escala \(\beta = 1000\). Encontre:
a proporção da população com renda entre 2000 e 4000 reais.
A renda media da população.
A renda mediana da população.
Solução. Seja \(X:\) Renda da população \(\sim\) Pareto(3,1000)
\(P(2000 < X < 4000) = F(4000) - F(2000) = \left(\frac{2}{4}\right)^3 - \left(\frac{1}{4}\right)^3 \approx 10.93 \%\)
\(E(X) = \frac{\alpha\beta}{\alpha - 1} = 1500\) reais.
É deixado como exercício ao leitor.
7.14 Distribuição de Weibull
Definição 7.16 Dizemos que uma variável aleatória \(X\) tem distribuição de Weibull com parâmetros \(\alpha > 0\) e \(\lambda > 0\) se sua função de densidade é dada por \[ f(x) = \lambda \alpha x^{\alpha - 1} e^{-\lambda x^\alpha}, \; x>0 \]
Notação: \(X\sim\) Weibull(\(\alpha,\lambda\)).
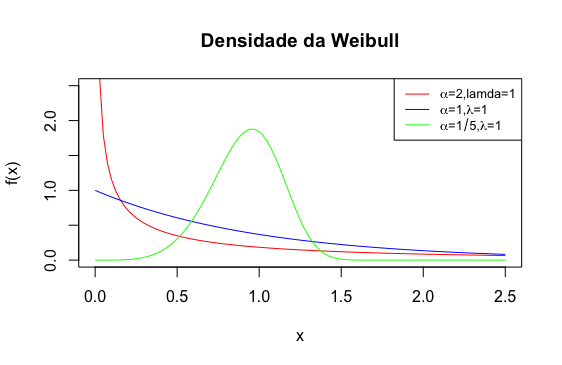
Observação. Quando \(\alpha = 2\) e \(\lambda = 1/\theta^2\) a distribuição é conhecida como distribuição de Rayleigh.
A função de distribuição de \(X\) é dada por
\[ F(x) = \begin{cases} 1-e^{-\lambda x^\alpha}, & x \geq 0 \\ 0, & x < 0 \end{cases} \]
Proposição 7.11 Seja \(X\sim\) Weibull(\(\alpha,\lambda\)), então
\[ E(X) = \lambda^{-1/\alpha} \Gamma(1+1/\alpha) \text{ e } Var(X) = \lambda^{-2/\alpha} \left[\Gamma(1+2/\alpha) - [\Gamma(1+1/\alpha)]^2)\right] \]
7.15 Distribuição de Laplace (dupla exponencial)
Definição 7.17 Dizemos que uma variável aleatória \(X\) tem distribuição de Laplace (ou dupla exponencial) com parâmetros \(\mu\in\mathbb R\) e \(\lambda>0\) se sua função de densidade é dada por \[ f(x) = \frac{1}{2} e^{-\lambda|x - \mu|}, \; x \in \mathbb R \] Notação: \(X\sim\) Laplace(\(\mu,\lambda\))
A função de distribuição de \(X\) é dada por
\[\begin{align*} F(x) = \begin{cases} \frac{1}{2} e^{\lambda(x - \mu)}, & x< \mu,\\ 1-\frac{1}{2}e^{-\lambda(x-\mu)}, & x\geq \mu \end{cases} \end{align*}\]
Proposição 7.12 Seja \(X\sim\)Laplace(\(\mu,\lambda\)), então \[E(X) = \mu \text{ e } Var(X) = \frac{2}{\lambda^2} \]